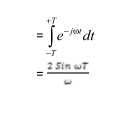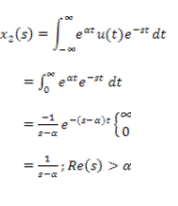Aplikasi Persamaan Integral Pada Penelitian
Integral dapat diaplikasikan ke dalam banyak hal. Dari yang sederhana, hingga aplikasi perhitungan yang sangat kompleks. Berikut merupakan aplikasi-aplikasi integral yang telah dikelompokkan dalam beberapa kelompok perhitungan. Penjelasan lebih lanjut dapat dilihat pada keterangan yang diberikan.
1. Aplikasi Integral pada sistem elektronik
Besarnya tegangan pada komponen elektronik dinyatakan sebagai berikut :
Karena komponen elektronik memiliki karakteristik seperti di atas maka analisis dari beberapa rangkaian elektronis harus diselesaikan menggunakan turunan maupun integral.
- Pada arus DC
Contoh :
Carilah persamaan tanggapan rangkaian berikut:
- Pada arus AC Biasa
Sebuah arus sinusoidal biasa direpresentasikan sebagai berikut :
Maka besarnya tegangan pada komponen elektronik menjadi
Maka pada rangkaian berikut tanggapannya adalah :
2. Transformasi-Transformasi
Transformasi yang akan dibahas di sini merupakan transformasi yang ada kaitannya dengan integral, yaitu transformasi Fourier dan Transformasi Laplace. Banyak transformasi dilakukan dengan prinsip integrasi terhadap bagian-bagian gelombang yang ada.
Mengapa perlu transformasi ?
- Setiap orang pada suatu saat pernah menggunakan suatu teknik analisis dengan transformasi untuk menyederhanakan penyelesaian suatu masalah [Brigham,1974]
- Transformasi dilakukan agar domain penelitian dapat diubah ke dalam domain penelitian yang lebih gampang sehingga dapat diselesaikan secara matematis dengan mudah. Contohnya transformasi Fourier dan Laplace mengubah sinyal dalam kawasan waktu ke kawasan frekuensi.
- Transformasi juga diperlukan bila kita ingin mengetahui suatu informasi tertentu yang tidak tersedia sebelumnya
-jika ingin mengetahui informasi frekuensi kita memerlukan transformasi Fourier
- Transformasi Fourier
Pada tahun 1822, Joseph Fourier, ahli matematika dari Prancis menemukan bahwa: setiap fungsi periodik (sinyal) dapat dibentuk dari penjumlahan gelombang-gelombang sinus/cosinus.
Penjelasan:
- 1 gelombang sinus dgn frek 50Hz dikatakan memiliki 1 frekuensi atau 1 spektrum frekuensi sinyal sinus dengan formula : 5sinus(50Hz) + 4sinus(20Hz) + 2 sinus(10Hz) dikatakan memiliki 3 spektrum frekuensi. Penjumlahan sinyal-sinyal tersebut nantinya akan membentuk sebuah sinyal baru.
- Sinyal kotak adalah penjumlahan banyak sinyal sinus yang memiliki frekuensi berbeda, dan banyaknya adalah infinity : tak terbatas.
Contoh :
Sinyal kotak merupakan penjumlahan dari fungsi-fungsi sinus berikut
f(x) = sin(x) + sin(3x)/3 + sin(5x)/5 + sin(7x)/7 + sin(9x)/9 …,
hasilnya sebagai berikut:
Kita dapat menyatakan semua sinyal periodik dalam penjumlahan fungsi-fungsi sinus-cosinus,
dengan cara :
Rumus FT kontinu 1 dimensi
Rumus sinyal kontinyu berhubungan erat dengan aplikasi integral
- Rumus FT diskret 1 dimensi
2. Transformasi Laplace
Bila transformasi Fourier direpresentasikan dalam kawasan frekuensi berlambangkan ) (ω , maka representasi gelombang/sinyal pada transformasi Laplace diubah ke dalam kawasan frekuensi X(s), di mana ω σ j s + = . Transformasi Laplace merupakan jabaran dari transformasi Fourier. Penjabaran ini dilakukan agar hitungan yang dihasilkan lebih sederhana dan lebih mudah. Tranformasi Laplace merupakan transformasi yang mengandung pasangan Transformasi Fourier kompleks yaitu X(s). Juga biasa disebut transformasi Laplace bilateral atau transformasi Laplace dua sisi (two-sided).
Contoh soal:
3. Aplikasi Integral untuk menghitung Volume
- Volume
Misal diberikan permukaan z=f(x,y) dan R merupakan daerah terletak pada bidang XOY atau bisa merupakan proyeksi dari permukaan z=f(x,y), maka volume benda ruang yang dibatasi diatas oleh permukaan z=f(x,y) dan di bawah dibatasi oleh R dituliskan
Contoh:
Hitung volume bangun ruang yang terletak di oktan pertama yang dibatasi oleh bidang
2x+3y+Z-6 = 0.
Jawab:
Dilihat dari gambar setelah bidang diproyeksikan terhadap bidang XOY diperoleh :
Maka volume bangun ruang dinyatakan sebagai berikut :